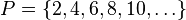Tareas de Probabilidad Y Estadísticas.
Operaciones con conjuntos.
Operaciones con tres conjuntos
En un diagrama de Venn, las posiciones relativas de tres conjuntos pueden ser muy variadas.
% elementos que no pertenecen a ningún conjunto, excepto al universal (región gris);
% elementos que pertenecen a un solo conjunto (regiones roja, amarilla y azul);
% elementos que pertenecen a dos conjuntos (regiones anaranjada, verde y violeta); y
% elementos que pertenecen a los tres conjuntos (región marrón).
Es decir, la disposición más general es la que define ocho regiones. En ninguna otra se llega a esta cantidad. [La disposición 5, por ejemplo, tiene siete. Si los elementos de tres conjuntos pueden ser ubicados en el diagrama 5, también podrán ser ubicados en el diagrama 12: una región
Obsérvese que la cantidad de regiones de cada clase se puede calcular aplicando la fórmula siguiente:
Donde ntc es el número total de conjuntos y ncs es el número de conjuntos que se solapan (superponen) en las regiones en cuestión. Por ejemplo, en un diagrama de tres conjuntos ntc = 3, la cantidad de regiones donde no hay conjuntos (ncs = 0) es 3!/[0! (3-0)!] = 1 (gris); la cantidad de regiones donde hay un solo conjunto (ncs = 1) es 3!/[1! (3-1)!] = 3 (roja, amarilla y azul); la cantidad de regiones donde se solapan dos conjuntos (ncs = 2) es 3!/[2! (3-2)!] = 3 (anaranjada, verde y violeta); y la cantidad de regiones donde se solapan los tres conjuntos (ncs = 2) es 3!/(3-3)! = 1 (marrón). El número total de regiones (colores) se puede obtener entonces aplicando la siguiente fórmula:
En otros términos, la cantidad de regiones surge de la construcción conocida como "Triángulo de Tartaglia". Los números de cada fila se obtienen sumando los dos adyacentes de la columna anterior
cantidad de
conjuntos
|
cantidad de regiones
Triángulo de Tartaglia
|
total de
regiones
|
0
1
2
3
|
1
1
1
1
2
1
1
3
3
1
|
1
2
4
8
|
Este procedimiento está justificado por el hecho de que las regiones están ordenadas en una estructura jerárquica del tipo "árbol": si en una región un conjunto se solapa con otros dos, se solapa también con cada uno de ellos, y ellos se solapan entre sí. La pregunta: « ¿Cuántas regiones hay donde se superponen ncs conjuntos?» es equivalente a la pregunta: « ¿Cuántos jefes tiene un empleado que se encuentra en el nivel ncs-ésimo de una escala jerárquica como la siguiente?»
Cada jefe vale por el número de superiores que tiene.
La tabla siguiente muestra distintas formas de identificar las regiones
La última columna contiene las ternas ordenadas correspondientes a cada una de las ocho regiones. Las tres componentes indican, respectivamente, si los elementos pertenecen (1) o no (0) a los conjuntos A, B y C.
El resultado de una operación con tres conjuntos es, gráficamente, una parte del diagrama que los representa (en el caso más general, el diagrama 12 de la primera tabla). Cualquier región compuesta se puede expresar en términos de las ocho regiones elementales de la tabla anterior. En el cuadro siguiente se muestran algunos ejemplos
Sin embargo, como se observa en la notación alternativa (última columna), muchas veces es posible escribir expresiones más compactas. (Éste no es el caso de la operación 3.)
Unión de Conjuntos.
La teoría de conjuntos es una de las partes de la matemática que se ha desarrollado desde fines del siglo XIX. Ha introducido términos como pertenencia, inclusión, unión y otro. Su uso ha permitido indudablemente mejorar la precisión del lenguaje en áreas de conocimiento como la teoría de relaciones y funciones, la teoría de las probabilidades, entre otras.
Interacción de Conjuntos.
En otras palabras: Así, por ejemplo, si A = { a, b, c, d, e} y B = { a, e, i, o}, entonces la intersección de dichos conjuntos estará formada por todos los elementos que estén a la vez en los dos conjuntos, esto es: A B = { a, e}
La intersección de conjuntos se denota por el símbolo ∩ por lo que D = P ∩ C.
Diferencia de Conjunto.
En teoría de conjuntos, la diferencia entre dos conjuntos es una operación que resulta en otro conjunto, cuyos elementos son todos aquellos en el primero de los conjuntos iniciales que no estén en el segundo. Por ejemplo, la diferencia entre el conjunto de los números naturales N y el conjunto de los números pares P es el conjunto de los números que no son pares, es decir, los impares I:
Como no hay ningún número par que no sea un número natural, la diferencia P menos N no tiene ningún elemento, por lo que es el conjunto vacío. La diferencia entre dos conjuntos A y B se denota por A \ B ó A − B, por lo que: N \ P = I, y también P − N = ∅.
